For full text search please use the '?' prefix. e.g. ? Onboarding

Stratification

Stratification

Stratification is the process of dividing members of the population into homogeneous subgroups before sampling. In statistical surveys, when subpopulations within an overall population vary, it could be advantageous to sample each subpopulation (stratum) independently.

Stratification is a common technique used in Monte Carlo sampling to achieve variance reduction.

Goal estimate: E(Y)E(Y). The standard Monte Carlo approach is to sample YiY_{i} and compute E(Y)E(Y) as 1n∑Yi\frac{1}{n}\sum Y_{i} which has variance var(Y)/nvar(Y)/n

The basic idea of stratification is to divide the sampling region into strata, sample within each stratum separately (each has mean Yˉi\bar{Y}_{i}) and then combine results from individual strata together to give an overall estimate, which usually has a smaller variance than the estimate without stratification. The final estimate you get is ∑wiYˉi\sum w_{i}\bar{Y}_{i}

They should have the same expected value but lower variance when the means differ across strata.

The intuition is that the variance of Y can be decomposed into the within-strata variance and the between-strata variance, and the latter (between strata) is removed through stratification.

A good stratification is the one that aligns well with the un-derlying clusters in the data. By explicitly identifying these clusters as strata, we essentially remove the extra variance introduced by them.

Stratification in online experiments

In the online world, because we collect data as they arrive over time, we are usually unable to sample from strataformed ahead of time.

For example, if YiY_i is the number of queries from a user ii, a covariate XiX_i could be the browser that the user used before the experiment started.

In experiments (e.g t-test) you compare the means of two groups (Yˉ+c\bar{Y}+_{c} and Yˉ+t\bar{Y}+_{t}). We want to see variance reduction in the delta between the two groups, Yˉ+c−Yˉ+t\bar{Y}+_{c} - \bar{Y}+_{t}.

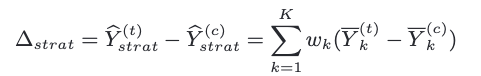
It is important to note that by using only the pre-experiment information, the stratification variable X (e.g which browser) is independent of the experiment effect. This ensures that the stratified delta is unbiased.

Backlinks