Programming for the Puzzled

MIT 6.S095 - Programming for the Puzzled

Lecture videos

Lecture notes

Puzzle 1. You Will All Conform. Trick

Array of people and they have caps on their head. These caps can be forward or backward.

0, 1, 2, 3, 4, 5, 6

F, B, F, F, B, B, F

We want all caps to conform, that is all are forward or all are backward. Possible operations: You can say to a person " Flip your cap". Or you can say "People from position from 2 to 3 flip your caps". Find minimum number of operations given an array of people with caps.

Simple solution is just to count forward and backward intervals

arr = ['F','B','F','F','B','F','F']

def solve(arr):
    forward, backward = [],[]
    i = 0
    while i < len(arr):
        j = i+1
        while j < len(arr) and arr[j] == arr[i]:
            j += 1
        if arr[i] == 'F': forward.append([i,j])
        else: backward.append([i,j])
    return min(len(forward),len(backward))

First person in line gives up what set of commands you will say to the people. For example if arr[0] = 'F', then you would say to all 'B-s' to flip their caps.

def please_all_conform(arr):
    arr.append('END')
    for i in range(1,len(arr)):
        if arr[i] != arr[i-1]:
            if caps[i] != caps[0]:
                print(f'Please people in positions {i}', end = '')
            else:
                print(f' through {i - 1} flip your caps!')

'Nuances with how you solve a problem and how you code it.'

Puzzle 2. The Best Time to Party. Line Sweep

Celebrities come at a party at particular times (intervals). When should you go to the party to max out the number of celebrities you will meet.

[('Beyonce',6,7), ('Taylor',7,9), ...]

Closed intervals on the left and open on the right.

Simple solution. Check all hours (starts and ends) and check how many intervals contain it. Depends on granularity of time

def solve(intervals):
    start = min([intervals[i][0] for i in range(len(intervals))])
    end = max([intervals[i][1] for i in range(len(intervals))])
    times = set(starts + ends)
    res = 0
    for t in range(start,end+1):
        res = max(res,count(t),intervals)
    return res

def count(t):
    return sum([ s <= t < e for s,e  in intervals])

'Lots of repeated computation = redundancy. Often you could reduce this redundancy by computing things incrementally.'

The only times that are interesting is when celebrities come and leave

The only time the result could change is if a celebrity enters or leaves.

Line sweep solution. Relies on the fact that the result would change only when you reach an event.

def solve(intervals):
    events = []
    for s,e in events:
        events.append((s,1))
        events.append((e,0))
    events.sort()
    res,curr = 0,0
    for time,is_start in events:
        if is_start:
            curr += 1
        else:
            curr -= 1
        res = max(res,curr)
    return res
# trick
def solve(intervals):
    events = []
    for s,e in events:
        events.append((s,1))
        events.append((e,-1))
    events.sort()
    return max(accumulate([p for _p in events]))

problem

Puzzle 3: You Can Read Minds. Encoding Information

Given a deck of 52 cards. William takes 5 cards at random and shows to Devas 4 of them. Devas uses an algorithm to determine the 5th card. He uses the info from the 4 cards he sees to guess the fifth card.

Show 4 cards, 5th card could be 1 of 48.

How many bits of information can 4 cards show? Use the order of the 4 cards gets you $4! = 24$. We have just 24 bits of information but have to encode 48. Ordering just uses the numbers on the cards, we need to use the suits.

Strategy: First card will give away the suit. By pigeonhole principle out of 5 cards there would be 2 with the same suits. The other 3 cards would give away the distance from the first card thinking in circular/modular computation.

Example: We pick King Diamond, A Diamond, 2 Spade, 3 Clubs, 5 Hearts.

William will hide the Ace and present K, 2, 3, 5.

Devadas sees King of Diamond, hence the hidden card is a diamond. 2,3,5 is the first permutation, hence the hidden card is 1 distance away from the Kind, that is and Ace.

Why this strategy works? The first card is the pivot card giving away the suit, hence there are 12 cards remaining that could possibly be the hidden card. we have 3 cards left t encode the 12 cards. Because we measure distance only in clockwise direction we are covered.

Is it possible to pick 4 random cards, hide one of it and encode it using the rest 3.

Article

Puzzle 4: Please Do Break the Crystal. Strategy + Flip problem statement

Problem statement:

You are given two identical crystal balls and you have access to a building with n floors labeled from 1 to 128.

You know that there exists a floor f where $0 <= f <= 128$ such that any egg dropped at a floor higher than f will break, and any egg dropped at or below floor f will not break.

In each move, you may take an unbroken egg and drop it from any floor x (where $1 <= x <= 128$). If the egg breaks, you can no longer use it. However, if the egg does not break, you may reuse it in future moves.

Return the minimum number of moves that you need to determine with certainty what the value of f is.

Links to problem: medium with two balls only.

hard with arbitrary number of balls.

Thinking

Binary search strategy - begin with first drop at 64. Worse case is if it breaks and then we have to do [1,63] = 63 drops more: total 64 drops.

Improvement: Use smaller interval - drop from 16, 32, 48, 64... Worse case if it breaks at 128 and we have to do 128/16 + 15 = 23 total drops

Even better: be around square root. Strategy start dropping first ball at floors: $k, 2k, 3k, .... n//k * k$ Worse case is if the first drop does not break until the end. Total drops = $n/k + k-1$. Goal is to minimize this function.

Take derivative and set to 0 -> $k = sqrt(n)$ Total worse number of drops is $2sqrt(n)-1$

So using this strategy of throwing on equal interval range $k, 2k ,...$ best is to choose k = sqrt(n) and total worse case is $2sqrt(n)-1$

However even more optimal strategy is to have decreasing intervals. They should get smaller as the problem gets easier.

Math Solution: Suppose least number of worse case throws is $x$. Then the highest floor from which you can drop first egg is from floor $x$. If you drop it from floor $x+1$ and it breaks then you'd have $x+1$ throws in total

Second drop can be highest from $x + x-1$. If you drop it from x+x, then your worse case would be $>=$ if the egg breaks from second drop + try drops from x+1..2x-1 -> total: $2 + x-1 = x+1$

Similarly kth drop should be from drop $x + (x-1) + (x-2) .. + (x-k+1)$.

Total number of drops would be: x + (x-1) + (x-2) + ... + 1 >= n x(x+1)/2 >= n

NB: MIT solution does not give the most optimal one. It assumes equal intervals for 2 balls and for the general case.

Another Math Solution:

Reverse engineer problem Given T moves and 2 balls find how many floors I can cover Find smallest T with which we can cover n floors

For k balls:

f(T,k) = 1 + f(T-1,k-1) + f(T-1,k)
f(T,2) = 1 + f(T-1,1) + f(T-1,2)
f(T,2) = 1 + T-1 + f(T-1,2)
f(T,2) = T + f(T-1,2)
f(T,2) = T + T-1 + T-2 + ... 1
f(T,2) = T*(T+1)/2

The above solution gives you O(nk) coding solution to the problem.

Remark

Moreover, it can be shown that $f(T,k)=C^{1}_{T}+⋯+C^{k}_{T}$ and using this information, problem can be solved in $O(k log n)$, using binary search.

Problem 5 & 6: Keep those queens apart. Backtracking (Recursion)

These two lectures consider the 8-queens problem. Lecture 5 gives overview and iterative solution of the problem. Lecture 6 gives recursive/backtracking solution.

Example. Find greatest common divisor.

Euclid's algorithm.

def iterative_gcd(m, n):
    while n > 0:
        m, n = n, m % n
    return m

def recursive_gcd(m, n):
    if m % n == 0: return n
    return recursive_gcd(n, m%n)

'You always get intuition about the problem by shrinking it and looking at small cases.'

Given $n$x$n$ board return the number of different ways we put $n$ queens on the board. link

Solution Represent a board using just an array where $j$-th element shows on which row we have a queen in column $j$. Exploit the fact there can be at most one queen in a single column.

class Solution:
    def totalNQueens(self, n: int) -> int:
        def is_safe(i,j,board):
            if i in board: return False
            for col in range(j):
                if abs(col-j)==abs(i-board[col]): return False
            return True
        def backtrack(j):
            nonlocal res
            if j == n:
                res += 1
                return
            for i in range(n):
                if is_safe(i,j,board): # pruning
                    board[j] = i
                    backtrack(j+1)
                    board[j] = None
        res,board = 0,[None]*n
        backtrack(0)
        return res

There is no closed form solution depending on $n$.

Problem 7: Tile that Courtyard, Please. Divide and Conquer (Recursion).

Problem. Consider a $2^n$x$2^n$ courtyard and $L$-shaped tiles (three square-tiles). Can you fill it in with $L$-tiles perfectly? No, total number of squares is $2^{2n}$ and is not divisible by 3. Then we change the problem and put a ban on one of the squares in the courtyard. Total number of squares is $2^{2n}-1$ which is divisible by 3.

Divide and Conquer Solution:

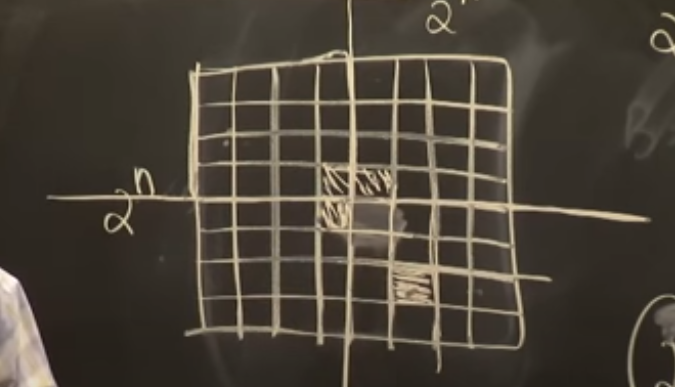
There is always a perfect tiling of the courtyard!

#Programming for the Puzzled -- Srini Devadas
#Tile that Courtyard, Please
#Given n in a 2^n x 2^n checkyard with a missing square at position (r, c), 
#find tiling of yard with trominoes (L-shaped dominoes).
#This version works directly on the given grid, and does NOT make copies
#of the grid for recursive calls.

EMPTYPIECE = -1



#This procedure is the main engine of recursive algorithm
#nextPiece is the number of next available tromino piece
#The origin coordinates of the yard are given by originR and originC
def recursiveTile(yard, size, originR, originC, rMiss, cMiss, nextPiece):

    #quadrant of missing square: 0 (upper left), 1 (upper right),
    #                            2 (lower left), 3 (lower right)
    quadMiss = 2*(rMiss >= size//2) + (cMiss >= size//2)
    
    #base case of 2x2 yard
    if size == 2: 
        piecePos = [(0,0), (0,1), (1,0), (1,1)]
        piecePos.pop(quadMiss)
        for (r, c) in piecePos:
            yard[originR + r][originC + c] = nextPiece
        nextPiece = nextPiece + 1
        return nextPiece

    #recurse on each quadrant
    
    for quad in range(4):
        #Each quadrant has a different origin
        #Quadrant 0 has origin (0, 0), Quadrant 1 has origin (0, size//2)
        #Quadrant 2 has origin (size//2, 0), Quadrant 3 has origin (size//2, size//2)
        shiftR = size//2 * (quad >= 2)
        shiftC = size//2 * (quad % 2 == 1)
        if quad == quadMiss:
            #Pass the new origin and the shifted rMiss and cMiss
            nextPiece = recursiveTile(yard, size//2, originR + shiftR,\
                originC + shiftC, rMiss - shiftR, cMiss - shiftC, nextPiece)

        else:
            #The missing square is different for each of the other 3 quadrants
            newrMiss = (size//2 - 1) * (quad < 2)
            newcMiss = (size//2 - 1) * (quad % 2 == 0)
            nextPiece = recursiveTile(yard, size//2, originR + shiftR,\
                            originC + shiftC, newrMiss, newcMiss, nextPiece)


    #place center tromino
    centerPos = [(r + size//2 - 1, c + size//2 - 1)
                 for (r,c) in [(0,0), (0,1), (1,0), (1,1)]]
    centerPos.pop(quadMiss)
    for (r,c) in centerPos: # assign tile to 3 center squares
        yard[originR + r][originC + c] = nextPiece
    nextPiece = nextPiece + 1

    return nextPiece

#This procedure is a wrapper for recursiveTile that does all the work
def tileMissingYard(n, rMiss, cMiss):
    #Initialize yard, this is the only memory that will be modified!
    yard = [[EMPTYPIECE for i in range(2**n)]
            for j in range(2**n)] 
    recursiveTile(yard, 2**n, 0, 0, rMiss, cMiss, 0)
    return yard

#This procedure prints a given tiled yard using letters for tiles
def printYard(yard):
    for i in range(len(yard)):
        row = ''
        for j in range(len(yard[0])):
            if yard[i][j] != EMPTYPIECE:
                row += chr((yard[i][j] % 26) + ord('A'))
            else:
                row += ' '
        print (row)


printYard(tileMissingYard(3, 4, 6))
printYard(tileMissingYard(4, 5, 7))

Problem 8: You Won't Want to Play Sudoku Again. Recursive search

Problem Given a sudoku grid, find a solution to it. problem

class Solution:
    def solveSudoku(self, board: List[List[str]]) -> None:
        """
        Do not return anything, modify board in-place instead.
        """
        def get_empty(board):
            for i,j in product(range(9),range(9)):
                if board[i][j] == '.': return (i,j)
            return -1,-1

        def possible(i,j,board):
            return set(list(map(str,range(1,10)))) - box(3*(i//3),3*(j//3)) - row(i) - col(j)

        def box(i,j):
            return set(board[i+di][j+dj] for di,dj in product(range(3),range(3)))

        def row(i):
            return set(board[i][j] for j in range(9))

        def col(j):
            return set(board[i][j] for i in range(9))

        def solve():
            i,j = get_empty(board)
            if i == -1: return True
            values = possible(i,j,board)
            for val in values:
                board[i][j] = val
                if solve(): return True
                board[i][j] = '.'
            return False

        solve()

Whenever you do a recursive search you need to clean what you did (line board[i][j] ='.') - this we call backtracking.

The above solution does not do any implications (row and column scans, boxes etc.) It is not the way you would solve sudoku in your head. The poss() function gives you potential values to fill in and you just do blind guessing. We want to integrate human approach in the algo - implications!

        def make_implications(board,i,j,e):
            board[i][j] = e
            impl = [(i,j)]
            can_imply,start = False,True
            while can_imply or start:
                start,can_imply = False,False
                for i,j in product(range(9),range(9)):
                    if board[i][j] =='.':
                        poss = possible(i,j,board)
                        if len(poss)==1:
                            x = poss.pop()
                            impl.append((i,j))
                            board[i][j] = x
                            can_imply = True
            return impl
        
        def undo_implications(board,impl):
            for i,j in impl:
                board[i][j] = '.'
    
        def solve():
            i,j = get_empty(board)
            if i == -1: return True
            values = possible(i,j,board)
            for val in values:
                impl = make_implications(board,i,j,val)
                if solve(): return True
                undo_implications(board,impl)
            return False
        
        solve()

Problem 9: The Disorganized Handyman. Sorting

Problem You have 100 unique nuts and 100 unique bolts, where each bolt has its own unique nut. All nuts and bolts are in a bag. Find all nut-bolt pairs.

Allowed operation:

• take one nut and take one bolt. If nut is bigger than bolt, then the bolt would go through the nut. If the bolt is bigger, then you cannot put the bolt in. IF nut fits the bolt then done!

Naive solution. $O(n^2)$ using brute force.

Can't compare the size of nuts to nuts. Can't compare the size of bolts to bolts.

Solution. Divide and Conquer - Quick Sort pivoting idea.

QuickSort and Merge sort are Divide and Conquer algorithms.

MergeSort requires $O(n)$ space and $O(nlogn)$ runtime.

Randomized QuickSort requires $O(1)$ space and $O(nlog)$ runtime on average. Worse xas is $O(n^2)$

QuickSort can be done in-place, whereas MergeSort cannot.

Problem 10: A Weekend To Remember. Graph

Problem. Nodes are friends. Edge between nodes implies a 'dislike' relation. Your job is to keep your friends happy. You organize 2 parties such that:

• each friend comes to exactly one party
• no pair of friends who dislike each other come to the same party

This is bipartite matching problem. Purpose of this puzzle is to say if you can do that or not.

Bipartite graphs are those which you can split in two groups of nodes and all edges have one end in one of the groups and the other edge in the other group.

Leetcode Leetcode

Bipartite graph = 2-colorable (color vertices such that no edge has two same color edges) = graph with no odd-cycles

class Solution:
    def isBipartite(self, graph: List[List[int]]) -> bool:

        def is_two_color(white,black):
            for u in range(n):
                for v in graph[u]:
                    if u in white and v in white: return False
                    if u in black and v in black: return False
            return True
        def colorize(s,is_black):
            if is_black: black.add(s)
            else: white.add(s)
            visited[s] = True
            for u in graph[s]:
                if not visited[u]:
                    colorize(u,1-is_black)
        n = len(graph)
        visited,black,white = [False]*n,set(),set()
        for s in range(n):
            if not visited[s]:
                colorize(s,True)
        return is_two_color(white,black)

Never depend of order of keys in a dictionary. Different looping through the same dictionary may give different order.

Problem 11: Memory Serves You Well. Dynamic Programming

Problem. Given array of coins, pick coins to maximize total value subject to constraint:

• if you pick a coin you cannot pick the next one. Leetcode

class Solution:
    def rob(self, nums: List[int]) -> int:
        @cache
        def dp(i,can_rob):
            if i == len(nums): return 0
            if not can_rob: return dp(i+1,True)
            return max(dp(i+1,False)+nums[i],dp(i+1,True))
        return dp(0,True)